Disjoindre le sujet et l’objet, le sujet actif et l’acte, l’acte et ce qu’il produit : n’oublions pas que c’est une simple sémiotique qui ne désigne rien de réel. La mécanique, science du mouvement, traduit déjà les faits dans le langage des humains.
[...]
Nos sens ne nous révèlent jamais le simultané, mais toujours le successif. L’espace et les lois humaines de l’espace supposent la réalité et la permanence d’images, de formes, de substances ; cela revient à dire que notre espace s’applique à un monde imaginaire.
[...]
C’est miracle que les hypothèses de la mécanique suffisent à nos besoins (machines, ponts, etc.) ; c’est une preuve que ce sont des besoins très grossiers et que les "petites erreurs" n’entrent pas en ligne de compte.
Pour ne pas remonter jusqu'à l'antiquité, rappelons simplement que René Descartes a fait progresser l’optique, en pensant la lumière comme vibration de l’éther invisible. Il a eu de plus le mérite d’introduire, en mécanique, l’idée fructueuse de quantité de mouvement Q, dont la conservation serait démontrée par Huygens :

1. La physique d'Isaac Newton
Mais pour expliquer les phénomènes gravitationnels, il a déliré des tourbillons invisibles dans l’éther, qui allaient obséder trop de ses contemporains. Heureusement, Isaac Newton allait pouvoir leur offrir une issue insoupçonnée, en partant des travaux de Galilée. Il énonça trois lois qui définissaient objectivement les forces physiques par vecteurs mathématiques :
1. Dans un référentiel inertiel, donc galiléen, le centre d’inertie d’un corps persiste dans son état de repos ou de mouvement rectiligne uniforme tant qu’il est isolé des forces extérieures ou que leur somme s’annule.
2. Si la somme des forces extérieures n’est pas nulle, elle est égale à la masse que multiplie le vecteur accélération du centre d’inertie (accélération qui n'est pas nulle puisque le centre d'inertie n'est ni au repos ni en mouvement rectiligne uniforme).
3. Si un corps A applique une force F(A/B) sur le corps B, le corps B applique sur le corps A une force F(B/A) de même direction, celle de la droite (AB), de même intensité et de sens opposé.
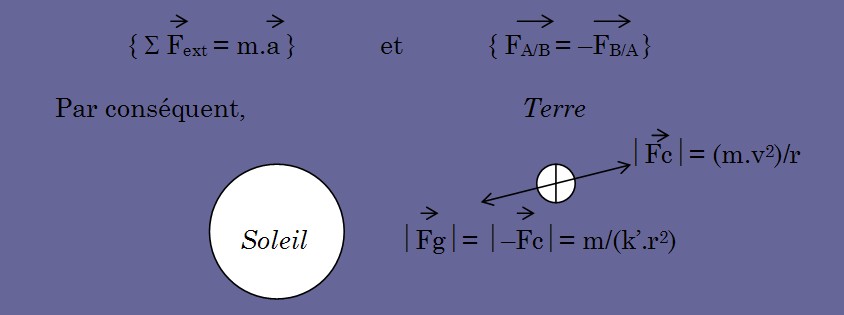
La terre, de masse m, gravitant autour du soleil à une vitesse v et à une distance r, est soumis à une force centrifuge { Fc = (m.v2) / r } qui tend à la pousser vers l’extérieur. Puisqu’elle ne s’éloigne pas, nous sommes tentés de penser que c’est parce que la force de gravité Fg s’oppose à cette force, donc qu’elle soit égale à –Fc. Or, la troisième loi de Kepler nous dit que le carré de la période T de révolution annuelle d’une planète autour du soleil est proportionnelle au cube de son rayon. Par calcul du périmètre circulaire parcouru à la vitesse v : { T = 2π.r/v }
Soit k Є ℝ,
T2 = k.r3 → k.r3 = (2π)2.(r2/v2)
Soit k’ = k/(2π)2,
r/v2 = k’.r3 → v2/r = 1/(k’.r2)
C’est de cette manière que Newton en vint à penser que la force de gravité devait s’exprimer proportionnellement à l’inverse du carré de la distance entre les corps. Il s’agit pourtant au départ d’une erreur grossière, celle de considérer la terre en tant qu’objet inertiel, alors que cette sphère n’est ni en repos, ni animée d’un mouvement rectiligne uniforme, et que les forces centrifuges/gravitationnelles ne constituent pas une couple action/réaction. Mais, du fait de considérer les objets célestes comme des objets communs, cette approximation lui avait fourni une bonne base de travail, qui lui permit d’exprimer le célèbre :
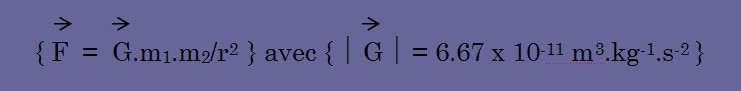
Les phénomènes ondulatoires ne concernent d’ailleurs pas que la lumière, mais aussi les phénomènes sonores ou électriques. Au XIXe, les ondes électromagnétiques de James Clerk Maxwell portèrent ombrage aux théories de Newton. En effet, si l’on suppose une particule d’une charge électrique q1, elle engendre aussitôt un champ magnétique B1, qui est perpendiculaire à sa vitesse v1. Si une deuxième particule la croise, sans la percuter, les forces électriques, par la proximité, { Fe1 ; Fe2 } sont égales et opposées, en accord avec la loi d’action/réaction. Mais, selon la théorie de Maxwell, il est possible que l’une d’entre elles seulement soit affectée par le champ magnétique de l’autre, il peut donc n’y avoir qu’une force magnétique { Fm }. On fait plusieurs expériences pour mesurer G, on trouve toujours le même résultat, donc G est une constante et la loi est valide. L’éther est devenu une hypothèse superflue, après la fusion conceptuelle des mécaniques terrestre et céleste. Tout est en mouvement. Les corps s’attirent naturellement et l’infinité du monde assure l’équilibrage des forces. Même si ce dernier point est insuffisant, qu’il demande l’ajout de forces anti-gravitationnelles discrètes, la théorie est opérationnelle et prédictive. Sur Terre, le calcul galiléen de la masse m par rapport au poids p est toujours valide, comme cas particulier de la gravitation d’un corps immobile sur le référentiel terrestre :
p = m.g
9.78 N/kg ≤ g ≤ 9.83 N/kg
Mais comment pouvait-on expliquer la lumière sans vibrations de la substance éthérée ? La lumière n’est pas à une hauteur graduée, elle est dans un cercle chromatique, répondit à cela Newton. La lumière blanche contient toutes les couleurs, comme on peut l’observer par la diffraction d’un prisme en laboratoire, ou celle des gouttelettes de pluie avec l’arc-en-ciel. La lumière est constituée de corpuscules se déplaçant en ligne droite, tant qu’ils ne sont pas déviés. La synthèse additive des couleurs engendre tous les intermédiaires, jusqu’au blanc de la lumière solaire. Les théories de René Descartes, puis de Christian Huygens, ne permettaient pas d’expliquer ces décompositions et recompositions des couleurs. Les hypothèses ondulatoires étaient-elles réfutées ?


